【理系決定版】数学の偏差値を30上げる参考書ルートと勉強法

数学に苦手意識を持っている、まだ数学を得意にできていない…”そんなお悩みをお持ちではありませんか?

授業にもついていけないし、まず何から始めればいいのか分からない…

苦手意識はなくなったけど、まだ得意だと言えるほどは数学力が身についてない…
筆者もかつて、中学レベルの数学知識も入っていない状態から学習を始め、試行錯誤を重ねてようやく、数学を克服することができました。
どうせ数学が得意な人は、理解力もあって数学のセンスが元からいい人なんだ!
そう思い込んでいましたが、受験数学はそんな理不尽な教科ではありませんでした。
今回の記事では、偏差値別に必要な数学の勉強法を紹介します。
これから紹介する内容を実践できれば、今よりも数学の偏差値が大幅にあがっているはずです。
✔︎ 偏差値が上がる数学の勉強方法
✔︎ 偏差値別のおすすめ数学参考書
✔︎ 挫折しづらい単元別の学習順序
不安を放置したらダメ!
「自分のペースで勉強を進めているけれど、今のままでは受かる気がしない…」というお悩みを抱えていませんか?
同級生は成績も上がってきているのに…
このような不安に駆られ、”勉強に集中ができなくなった、勉強習慣が崩れた”という人をたくさん見てきました。そんなお悩みを解消するために、大学受験を乗り越えるための7つの無料特典をご用意しました。
5年以上にもわたり1000人以上の受験生の悩みと向き合ってきた経験、さらには筆者自身の受験経験をもとにした、公式LINE限定の7大特典です。
気になる方は、以下から特典内容を確認のうえ、公式LINEをご登録ください。
偏差値が上がる数学の学習計画
数学の勉強で大事なのは、どの期間で何をどれくらい反復するかです。では、ここで皆さんに質問ですが、数学にセンスは必要だと思いますか。
正解は、数学にセンスは必要です。ただ、ここでいうセンスとは生まれつきの才能のことではありません。センスとは、いかに知識を使いこなせるまで実践を重ねたか、つまりいかに泥臭い努力をしたかです。
では、泥臭い努力とはなにか。その正体こそが、先ほど紹介した「どの期間で何をどれくらい反復するか」です。

参考書1周分を終わらせることを最初の目標にしよう!
反復学習に必要な3ステップ
これは、仮に目標が参考書1周の完走だとすると、達成すべき量はその参考書のページ数になります。
参考書を進める時、1時間あたりの進み具合は人によって異なります。
達成するべき量と1時間あたりに進められる量が決まれば、達成までにかかる勉強時間が導き出されます。もし達成期間が決まっていれば、その日数で割ると1日の数学の勉強時間がわかるし、1日の数学の勉強時間が決まっていれば、達成にかかる期間がわかります。
| 参考書のページ数 | 300 p |
| 1hで進むページ数 | 5 p |
| 達成したい期間 | 20日 |
| 数学の勉強時間 | 1日3時間 |
初学者の場合、最初の基礎参考書は1ヶ月で1周程度のペースで進めると続きやすい
1周目の計画が立てられたら、あとは2周目・3周目と同様に勉強計画を立てられるので、一番の鬼門となるのは参考書1周目です。
あくまで経験則ですが、2周目は1周目の7割ほど、3周目は1周目の5割ほどの労力で反復することができるので、まずは1周目を終わらせましょう。
数学の参考書1周目の勉強法
数学が苦手で嫌いな人の場合、気をつけなければいけない以下2つの注意点があります。
✔︎ 不明な問題はすぐ解答を見る
✔︎ 最初は暗記する意識で進める
すでに基礎力のある人が参考書で腕試しをするなら話は別ですが、基礎が身についてない数学苦手者が参考書を進める場合、いくら考えたところで正解は浮かんできません。
もし初学者が早めに成績を上げたいのなら、いかに早く基本的な解法パターンを頭に入れられるかがポイントになります。

でも、数学は根本原理の理解と応用力が重要ってよく聞くけど…
最終的には、解法の原理理解と応用力が数学の得意不得意を分けます。しかし、それはやるべき基礎知識をつけた、ある一定レベルまで達した人がやる次のステップです。
ですので、基礎知識がまだ身についてない人は、以下の手順に沿ってまずは基礎知識のインプットから始めましょう。
どのように解けばよいか20秒以内に方針が立たない場合は、すぐに解答を見ましょう。
公式や定義がわからない場合は、単元はじめの説明を読み直します。解き方がわからない場合は、解説を読んで理解したら、理解した内容を含めて、その問題の解き方を誰かに教えるように、先生になりきって声に出して説明してみましょう。
その問題の解説が説明できたら、解説を隠して自力で解けるまで繰り返し書いて解き、その問題の最初から最後まで自力で解けたら、そこで初めて次の問題に移るようにしましょう。
この手順で参考書を進めれば、一時的に記憶として解法パターンが身につきます。
ただし、これは一時的な記憶ですので、2周目3周目と反復を重ねることで、完全な定着をさせていきましょう。
数学の参考書2周目の勉強法
参考書2周目は、以下のように1周目の時と少し異なる立ち回りをします。
✔︎ 参考書の2周目は思い出す作業
✔︎ 解ける問題と解けない問題を分類
参考書の2周目は、主に1周目で覚えた内容を思い出す工程だと思ってください。当然1周だけでは記憶は定着しないため、自力で解ける問題と解けない問題に分かれてきます。
どれが解ける問題で、どれが解けない問題かを分類するのが、2周目のもうひとつの役割です。

2周目はつまらないと感じやすい工程なので忍耐する覚悟が大切!
どのように解けばよいか1分以内に思い出せない場合は、すぐに解答を見ましょう。
自力で解き方を思い出し、解法の過程を最後まで書いて解けた場合は、問題文の上や横のスペースに○を1つ書き加えましょう。
自力で解けなかった場合、解けなかった原因が「公式や定義を覚えていなかったから」であれば、単元はじめの説明を読んで覚え直しましょう。
解けなかった原因が「解く方針が思いつかなかったから」であれば、解説を読んで理解した後に、理解した内容を含めてその問題の解き方を誰かに教えるように、声に出して説明してみましょう。
単元はじめの説明を読んで覚え直したら、または問題の解説が説明できたら、解説を隠して自力で解けるまで繰り返し書いて解いてください。その問題の最初から最後まで自力で解けたら、そこで初めて次の問題に移るようにしましょう。
2周目が完了すれば、参考書の半分ほどの解法が身についてきます。ただし、この段階ではまだ、模試やテストでの得点にはつながりません。

この問題、どこかで見たことはある気がするけど、解き方が思いつかない…
模試やテストの時に経験するこの現象は、参考書2周目のような中途半端な状態で終わってしまった時によく発生します。
数学の参考書3周目以降の勉強法
参考書の3周目以降も、基本的には2周目と同様ですが、以下の点が異なることに注意してください。
✔︎ 3つ◯がついた問題は一旦OK
✔︎ 全問題で◯が3つで参考書OK
参考書の3周目以降は、解ける問題も多くなるので比較的スムーズに進みます。また、この頃から数学に対する苦手意識も徐々に薄まってきます。

3周目以降は徐々に飽きが出てくるけど、かなり大切な工程なのでもうすこし耐えよう!
どのように解けばよいか1分以内に思い出せない場合は、すぐに解答を見ましょう。
自力で解き方を思い出し、解法の過程を最後まで書いて解けた場合は、問題文の上や横のスペースに○を1つ書き加えましょう。
自力で解けなかった場合、解けなかった原因が「公式や定義を覚えていなかったから」であれば、単元はじめの説明を読んで覚え直しましょう。
解けなかった原因が「解く方針が思いつかなかったから」であれば、解説を読んで理解した後に、理解した内容を含めてその問題の解き方を誰かに教えるように、声に出して説明してみましょう。
単元はじめの説明を読んで覚え直したら、または問題の解説が説明できたら、解説を隠して自力で解けるまで繰り返し書いて解いてください。その問題の最初から最後まで自力で解けたら、そこで初めて次の問題に移るようにしましょう。
自分が習得したい問題すべてに◯が3つ付けば、その参考書の解法パターンは頭に入っていることになります。ここまでの流れが完了すれば、次の参考書へと移りましょう。
ここまでの流れが習得できれば、模試で数学の偏差値が60前後まで伸びます。
数学の応用力をつける勉強法
ここまでの手順は、解法パターンを知識として身につける工程でした。ここからは、身につけた解法パターンを組み合わせる工程、いわゆる応用力を身につける工程になります。

ここから原理の根本理解と応用練習が必要な段階になるよ!
難関大学を志望する受験生の中には、このような勘違いをした人がいます。

基礎なんかできなくても、応用ができれば二次試験で点数とれるからテキトーでいいや…
残念ながら、応用は基礎ができていなければ身につくことはありません。
問題に対して解法Aだけでも解けるのが基礎問題、問題に対して解法A・B・C…を同時に用いないと解けないのが応用問題、という構造になっているからです。
つまり、基礎知識の完全定着こそが応用力につながるというわけです。
では、基礎知識の完全定着とはどういう状態か。それが、以下の3つの条件すべてをクリアしている状態になります。
数学の基礎が定着した状態とは
- 1. 解法パターンが身についているか
- 解法パターンについては、ここまでの過程を行なっていただければ身についているはずですので、ここまで読まれた方は気にしなくて構いません。
- 2. 類題を出されても自力で解けるか
- 類題が自力で解けるかどうかについては、終わらせた参考書と同レベルの参考書、あるいは同じ参考書内の類題を演習することで、確認をすることができます。
- 3. 他人にわかりやすく説明できるか
- じつは、この説明をする過程が多くの受験生の悩みポイントになっています。理解している状態なのかどうか、なかなか自分では判断ができないため、できている気になったまま放置してしまうからです。
そのような場合に客観的に判断する方法が、他人に解法をわかりやすく説明できるかどうかなのです。
ただ、説明する相手がいないという人もいるでしょう。そのような時は、自分自身が講師役と生徒役の一人二役になって、自分自身に説明をしてみてください。
❶ 講師役:解法の理由を説明する
❷ 生徒役:何度もなぜと聞き返す
これを繰り返していると、自分が理解できていない内容が浮き彫りになるので、嫌でも根本からの理解が進みやすくなります。
受験対策していますか?
「自分のペースで勉強を進めているけれど、今のままでは受かる気がしない…」というお悩みを抱えていませんか?
同級生は成績も上がってきているのに…
このような不安に駆られ、”勉強に集中ができなくなった、勉強習慣が崩れた”という人をたくさん見てきました。そんなお悩みを解消するために、大学受験を乗り越えるための7つの無料特典をご用意しました。
5年以上にもわたり1000人以上の受験生の悩みと向き合ってきた経験、さらには筆者自身の受験経験をもとにした、公式LINE限定の7大特典です。
気になる方は、以下から特典内容を確認のうえ、公式LINEをご登録ください。
数学を勉強するときの単元順
基本的には、参考書を前から順に勉強するというやり方で問題ないですが、以下の点に気をつけてください。
数学IAを勉強するとき
データの分析
主に共通テスト対策として学習すること、配点がそれほど高くないこと、学習範囲が限られていることから、苦手意識が強ければ後に回しても構いません。
ただし、数学Bの統計的な推測の基礎になることや(※二次で統計的な推測が出題される大学を選ぶ場合は注意)、共通テストの情報科目でも出題されるなど、さまざまな箇所で利用されることに注意が必要です。
数学と人間の活動
共通テストでは出題されないこと、二次試験でも出題される大学が限られていることから、必要のない人は飛ばしてもよい単元です。
また、必要とされる場合でも、この単元は概念的で難しい問題が多いので、数学の苦手意識が強いうちは一旦飛ばして、後から集中的に学習するというのでもよいでしょう。
集合と論理
主に共通テスト対策として学習すること、配点がそれほど高くないこと、学習範囲が限られていることから、苦手意識が強ければ後に回しても構いません。
ただし、共通テストだけでなく二次試験でも「集合と論理を絡めた問題」はよく出るので、数学に対する苦手意識が緩和された段階で、必ず克服するようにしましょう。
数学IIBCを勉強するとき
数列
Σ(シグマ)の本質的な理解と数学的な概念の把握が必要とされるため、苦手意識が強い受験生も多い単元です。特に難問になると、しっかりと理解をしていなければ完答にはつながりません。
最終的には克服しなければなりませんが、数学に苦手意識のある初学段階のうちは、深追いをしすぎない程度に学習を進めてよいでしょう。
統計的な推測
共通テストでは選択制のため、二次試験で当単元が出題される大学を受けない場合は、飛ばしてもよいでしょう。
文系理系問わず、統計学は大学以降の研究やキャリアを考えた時に非常に重要な学問になるので、時間的に余裕のある人は学習をしておいて損はしません。
ベクトル
共通ベクトルは苦手とする受験生が多いです。ベクトルの範囲における公式や定義は頭に入っているのに解けないという場合は、数学Aの「図形の性質」の単元や、数IIの「図形と方程式」の単元が苦手であることが多いので、該当する場合は先にそれらの単元を復習した方がよいでしょう。
数学IIIを勉強するとき
数学IAIIBが先
極限の範囲や微分積分など、数学IIIは数学IAIIBの延長になる単元がほとんどです。まだ数学IAIIBの基礎ができていない場合は、数学IIIに時間をかけてもなかなか定着しないので、先に数学IAIIBから優先的に固めましょう。
数学のおすすめ参考書ルート
ここでは、筆者(東工大卒)が受験時に使用した数学の参考書を紹介します。
偏差値39〜58のとき
| 使った参考書 | 青チャート |
| 解いた問題 | 例題★1〜★3 |
| 解き進め方 | ◯が3つつくまで反復 |
| 意識したこと | 短期間で一気に進める |
青チャートは、章末問題や★4〜★5以外はそれほど難易度は高くなく、解説も丁寧に書かれている網羅系参考書なので、時間を集中させて一気にやり込む参考書としてはおすすめです。数学があまり得意でない場合は、★1から取り組むようにしましょう。
また、青チャートだと分量が多すぎるという場合は、例題の★1〜★3のみに絞って学習を進めたり、頻出問題に絞った「基礎問題精講」のような参考書で代用したり、残された時間でできる進め方を選ぶとよいでしょう。
ただし、数学が大嫌いで苦手意識も強い人の場合は、最初に取りかかる参考書として、これらは難しく感じる可能性もあります。
数学嫌い向けの参考書①
数学は苦手だけれど、網羅系参考書で幅広く基礎を学びたいという場合は、チャート式の中でも初学者向けのレベルを揃えた「白チャート」がおすすめです。
注意点としては、網羅系参考書ということもあり、例題の分量が多いので、まずは★1〜★2まで身につける、その後★3〜★5を身につけるというように、段階を分けて学習をするとよいでしょう。
数学嫌い向けの参考書②
数学は苦手、かつ白チャートのような網羅系参考書を学ぶ時間がないという場合は、初学者向けのレベルのうち頻出度の高い問題を揃えた「入門問題精講」がおすすめです。
注意点ですが、紛らわしい解説の仕方をしている箇所もちらほら見られるため、数学が大の苦手という人は、質問ができる環境で取り組むとよいでしょう。
数学嫌い向けの参考書③
数学が大の苦手で大嫌い、もしくは従来の参考書は堅苦しくて頭に入ってこないという場合は、数学嫌い向けに語り口調で書かれた「初めから始める数学」がおすすめです。
ほかの初学者向けの参考書と同様に、取り組みやすい例題とわかりやすい解説が載っており、さらに単元はじめの解説が非常に丁寧に書かれています。
偏差値58〜60のとき
| 使った参考書 | クリアー数学 |
| 解いた問題 | 基本問題(A問題) |
| 解き進め方 | 演習をメインに進める |
| 意識したこと | 初見でも解けるか確認 |
青チャートの次にやった参考書は、教科書の傍用問題集です。これは、身につけた解法を使いこなせるかどうか、確認するステップになります。
今回でいうクリアー数学のように、2冊目以降にあたる参考書の場合、初見で解けた問題は反復しなくてかまいません。
代用できる参考書
筆者の学校ではクリアー数学でしたが、通っている学校によって配られる問題集は異なると思うので、ご自身の学校で配られた問題集で構いません。
在学中の場合、定期テストの対策にもなるので、学校で配られた問題集を用いた確認作業は非常におすすめです。
偏差値60〜64のとき
| 使った参考書 | 1対1対応の演習 |
| 解いた問題 | 例題のみ |
| 解き進め方 | 演習をメインに進める |
| 意識したこと | 解けない問題のみ反復 |
類題の演習後に学習する参考書は、難関大レベルを目指す場合のみで構いません。もし難関大学を目指すなら、1対1対応の内容は確実に解けるようにしておきたいところです。
該当する大学
旧帝大早慶・医学部・一科神(旧 一工神)を目指す場合は、1対1対応のすべての演習が必要になります。
また、これらに該当しない大学でも、筑波大学・横浜国立大学・千葉大学・東京理科大学など準難関大を目指す場合は、このレベルまでやっておくと安心です。
代用できる参考書
1対1対応の数学は王道の参考書ですが、6冊も揃えるのはしんどいという人もいるでしょう。その場合は、同等の代用できる参考書として「標準問題精講」が挙げられます。
入門問題精講、基礎問題精講と進めてきた人は、こちらの参考書の方が馴染みがあるかもしれません。
注意点としては、数学IAは比較的取り組みやすいですが、数学IIBと数学IIIが難しいというところ。特に、数学IIIは非常に難易度が高いので、準難関大志望の場合は、数IIIはやらずに過去問演習へと移るのがおすすめです。
偏差値64〜70のとき(筆者の場合)
| 使った参考書 | 大学への数学(黒) |
| 解いた問題 | 例題のみ |
| 解き進め方 | 演習をメインに進める |
| 意識したこと1 | 解けない問題のみ反復 |
| 意識したこと2 | 1問に多く時間を使う |
難関レベルの演習については、筆者の場合は大学への数学(黒)を選択しましたが、かなり古い参考書ですので、以下の参考書がおすすめです。
代用できるおすすめ参考書
これらの参考書は、実際の難関大学の二次試験で出されるような良質な難問揃いです。これまでの参考書のように「解法パターンを身につける」という目的で取り組むというよりも、身につけてきた解法知識をもとに、いかに喰らいつけるかを確かめる参考書です。
1問あたりに20〜30分ほど考え込む時間を設けてもよいので、思考してなんとか喰らいつく練習を積み重ねましょう。
また、別解や解説が豊富なので、もし自力で解けなかった場合でも、解答を見て自分なりに理解し、何度も血肉となるまで繰り返すことが大切です。
難関理系の+α参考書
東大・京大・東科大(旧 東工大)・阪大・早慶の理工・難関医学部など、難関大学を狙う受験生の場合は、頻出の単元対策として、以下の参考書がおすすめです。
それぞれ古い参考書ですが、今でも重宝できる非常に良質な参考書ですので、残された時間でできる量をピンポイントで進めてみるとよいでしょう。
| 解き進め方 | 演習と理解促進が目的 |
| 意識すること1 | 苦手な問題を中心に |
| 意識すること2 | 1問に多く時間を使う |
| 意識すること3 | 理解と考察に時間を使う |
+αの参考書は、必須ではありません。これらを除いても、それまでの演習がしっかりと身についていれば、どのレベルの大学でも合格ボーダー付近は狙える実力が身につきます。
ですので、あとは自身の大学の過去問分析と演習に時間を費やし、志望大学の応用のクセに対応できるようにしておきましょう。
数学の模試の復習方法
模試やテストの直しは非常に重要です。ここまでに紹介した内容の中で、最も大切な内容と言っても過言ではありません。もしこれらをおろそかにすると、どれだけ参考書演習を重ねていようと、途中で成績が伸び悩む段階がやってきます。
なぜなら、どこが自分の弱点なのかがわからないまま、勉強時間をかけることになるからです。テスト結果は等身大の自分を写してくれる鏡ですので、必ず行うようにしましょう。
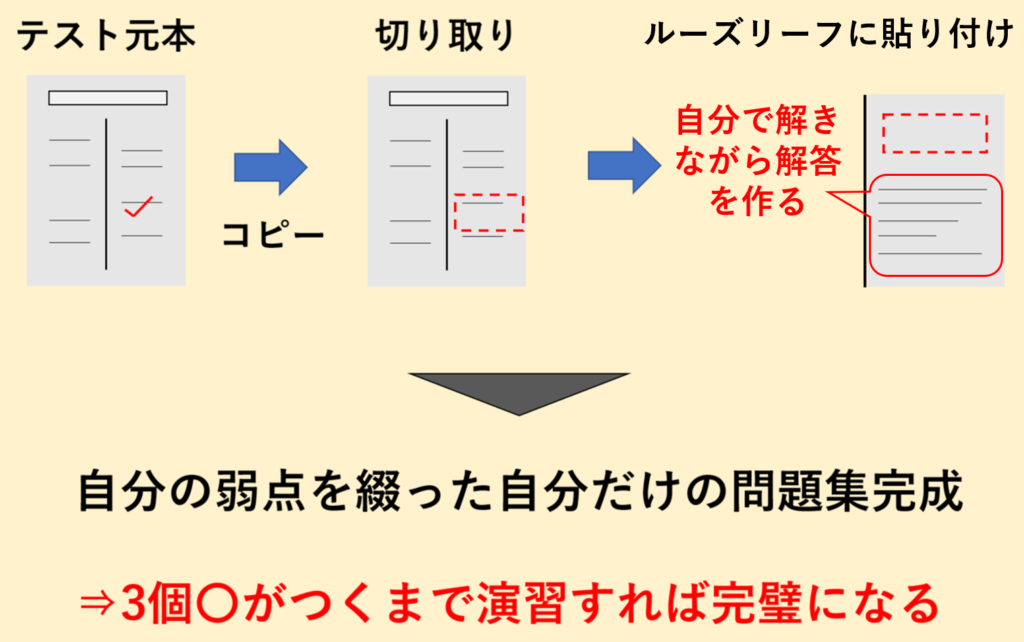
模試やテストの復習方法は以下の4ステップがおすすめ!
受け終わった模試やテストの問題用紙を印刷しましょう。
失点した箇所の問題文を切りとり、苦手克服用として専用のノートに貼りましょう。ただし、失点要因が単純なケアレスミスだった場合は、貼らなくて構いません。この場合は、その場で解き直し、自力で正解できるようにしましょう。
失点した箇所の解説を読んで理解ができたら、その理解したことをもとにして、自力で解答を作成しましょう。答えまで至る過程に加え、時間が経った後に見返してもピンとくるように、自分用のわかりやすいメモなどを加えながら作り込むとベストです。
単元❶〜❸までの一連の流れができたら、自分専用の苦手克服に使える参考書のできあがりです。定期的に復習して解けるようにすれば、苦手とする範囲が徐々になくなっていくため、成績が安定するようになります。
以上の流れが、数学を不得意から得意に変えるための、一連の学習ステップになります。数学は努力で克服できる教科ですので、ぜひ諦めずに実践して、数学を得点源に変えましょう。
今の合格可能性を診断
「今の勉強量のままで、第一志望に受かるのかな」など、今のパフォーマンスに不安を抱えていませんか?
ざっくりでも現在の合格可能性を知ることができたら…
現状がわからない中で勉強するのは、大きな不安とストレスを伴うものです。
そんな日々を奮闘する受験生向けに、1分で診断ができる「合格可能性診断」「合格に必要な勉強時間診断」をご用意しました。
今の自分と志望大学はどの程度かけ離れているのか、どれくらい勉強しなければならないのか。
目安を知りたい方は、以下のボタンタップからお手軽に診断してみてください。
今回の内容が参考になったという方は、下記の公式LINE登録から受験特典を受けとって、さらなる学習の向上に活かしてください。
基礎の徹底が超重要!
「自分のペースで勉強を進めているけれど、今のままでは受かる気がしない…」というお悩みを抱えていませんか?
同級生は成績も上がってきているのに…
このような不安に駆られ、”勉強に集中ができなくなった、勉強習慣が崩れた”という人をたくさん見てきました。そんなお悩みを解消するために、大学受験を乗り越えるための7つの無料特典をご用意しました。
5年以上にもわたり1000人以上の受験生の悩みと向き合ってきた経験、さらには筆者自身の受験経験をもとにした、公式LINE限定の7大特典です。
気になる方は、以下から特典内容を確認のうえ、公式LINEをご登録ください。



