【2025年最新】共通テスト数学で8割を超える勉強法を全ステップ解説

共通テスト数学で8割とりたいのに、このまま勉強しても伸びる気がしない…”そんな不安をお持ちではありませんか?

周りのライバルより対策が遅れたけど、今からでも間に合うかな…

共通テスト数学で8割とりたいけど、できるだけ最短で伸ばしたい…
共通テスト数学で高得点を狙っているのに、勉強しても思うように点数が伸びず、悩んでいる人は少なくありません。
実は、得点を伸ばすためには、大きく分けて4つのステップを踏む必要があります。現在の皆さんがどの段階で止まっているかによって、今後の対策は異なるのです。
勉強しているのに点数が伸びないのは、どこに原因があるのだろうか
そこで今回は、共通テスト数学で8割をとるために必要な対策を、4つの勉強ステップに分けて紹介します。
✔︎ 共通テスト数学8割までの4手順
✔︎ 今後やるべき具体的な勉強方法
✔︎ 共通テスト数学を解くテクニック
不安を放置したらダメ!
「自分のペースで勉強を進めているけれど、今のままでは受かる気がしない…」というお悩みを抱えていませんか?
同級生は成績も上がってきているのに…
このような不安に駆られ、”勉強に集中ができなくなった、勉強習慣が崩れた”という人をたくさん見てきました。そんなお悩みを解消するために、大学受験を乗り越えるための7つの無料特典をご用意しました。
5年以上にもわたり1000人以上の受験生の悩みと向き合ってきた経験、さらには筆者自身の受験経験をもとにした、公式LINE限定の7大特典です。
気になる方は、以下から特典内容を確認のうえ、公式LINEをご登録ください。
Step1 網羅系参考書を定着
共通テスト数学で8割を目指すには、大前提として基本的な知識を定着させる必要があります。では、その「基本的な知識」とは何でしょうか。
✔︎ 出題単元の定義と概念の理解
✔︎ 定理や公式の導出方法と理由
✔︎ 条件文ごとの解法パターン
共通テスト数学で8割を目指すために必要な知識は、上で示した3つです。これらを効率よく学習できるのが、網羅系参考書なのです。
基礎を固める網羅系参考書
網羅系参考書の例
チャート式(黄 or 青)
対象:黄 ★1〜★4 青 ★1〜★3
Focus Gold
対象:例題 ★1〜★3
New Action Legend
対象:例題 ★1〜★3
上記のいずれかを抜けなく定着させられたら、共通テスト数学に必要な最低限の知識は身につけられます。

網羅系参考書の勉強法は、以下の記事でくわしく解説しています
網羅系の代わりとなる参考書
網羅系の代わり
入門/基礎/標準問題精講
学校教科書+傍用問題集
マセマ【初め】~【合格】
まだ網羅系参考書も代わりの参考書も学習していない場合は、網羅系参考書をおすすめしますが、いずれかを用意して学習を進めましょう。

数学の具体的な勉強法は、以下の記事でくわしく解説しています
参考書が定着したか知る方法
参考書をただ演習したからといって、基本的な知識が必ずしも「定着」したとは限りません。以下に当てはまる場合は注意が必要です。
周回して解けるようにはしたものの、模試になると見覚えのある問題を完答できず、後から解答と解説を確認すると理解できるケース
定着度を確認する4ステップ
❶ 解法パターンは身についたか
「解法パターンが身についた」とは、参考書の例題をヒントなしで、記述過程まで含めて解ける状態を指します。
すべての例題が解けるようになって初めて、共通テスト数学で8割をとるために必要な「基本的な知識」が身についたといえます。
自信がない場合は、身につくまで繰り返し演習しましょう。
❷ 類題を出題されても解けるか
❶のステップをクリアした段階では、理解力が非常に高い人を除き、多くの場合「覚えた」と「理解した」が半々に混在した状態になります。
ここで学習を止めてしまうと、危険な代表例で紹介した「模試になると完答できない」状態に陥ります。
必ず、終わらせた例題と同レベルの類題に取り組み、自力で9割以上解けるかどうかを確認しましょう。
❸ 公式や定理を導出できるか
❶❷のステップをクリアした段階で、共通テストレベルの基本的な解法パターンは身につきます。
しかし、共通テスト数学の厄介な点は、単に解法パターンが身についているかどうかだけでなく、公式や定理の意味を問う問題も少なくないところです。
これに対応するには、各単元の公式や定理の導出(タップで移動可能)を理解しておくことが不可欠です。
❹ わかりやすく解説できるか
❶❷❸のステップをクリアした段階で、センター試験の数学なら8割を超える力は身についているでしょう。
しかし共通テスト数学では、文章を正しく読み取り、知っている解法パターンに落とし込む過程が求められます。
ここで必要なのが「原理の根本的な理解」です。その理解度を確かめるには、「人にわかりやすく説明(タップで移動可能)できるかどうか」を基準にすると明確です。
導出できるようにする公式と定理
共通テスト数学で8割を目指すうえでは、以下の公式や定理の導出を、ざっくりでも理解しておくとよいでしょう。
ただし、実戦で毎回導出していては時間が足りません。普段はすぐに活用できるように覚えておき、あくまで原理を理解しておくという位置づけです。
数学 I・II
| 三角比の基本公式 | 二項定理 |
| 加法定理 | 半角・二倍角・三倍角 |
| 1/6・1/12・1/3の公式 |
数学 A・B・C
| 三角形の五心 | メネラウスの定理 |
| 順列組合せの変形 | 数列の一般項と和 |
| ベクトル方程式 | ド・モアブルの定理 |
人にわかりやすく説明する勉強法
人にわかりやすく説明できるかどうかを確かめる方法としては、自分が講師役と生徒役を一人二役で演じ、自分自身に説明してみるのが効果的です。
❶ 講師役:解法の理由を説明する
❷ 生徒役:何度もなぜと聞き返す
これを繰り返す中で、うまく説明できなかったり、つい誤魔化そうとする箇所が出てきたら、そこが理解できていない内容です。
時間をかけてよいので、「なぜ」に答えられるよう、丁寧に調べて考え、原理からの理解を深めましょう。
受験対策していますか?
「自分のペースで勉強を進めているけれど、今のままでは受かる気がしない…」というお悩みを抱えていませんか?
同級生は成績も上がってきているのに…
このような不安に駆られ、”勉強に集中ができなくなった、勉強習慣が崩れた”という人をたくさん見てきました。そんなお悩みを解消するために、大学受験を乗り越えるための7つの無料特典をご用意しました。
5年以上にもわたり1000人以上の受験生の悩みと向き合ってきた経験、さらには筆者自身の受験経験をもとにした、公式LINE限定の7大特典です。
気になる方は、以下から特典内容を確認のうえ、公式LINEをご登録ください。
Step2 センター過去問で実戦
センター試験の過去問で8割を安定して得点できるようになれば合格とする
Step1で解法の定着と理解は図れたものの、実際の試験で解けるかは別問題です。解法が本当に身についているかを確かめる手段として、センター試験の数学を活用します。
① 時間制限なしで8割を目指す
まずは、時間制限を設けずにセンター試験の数学に取り組み、身につけた解法を正しく使えるかを確認しましょう。
時間的焦りがないはずなので、できるだけ検算を行い、ケアレスミスをなくしましょう。
時間制限なしで8割をとれない場合、失点が大きい単元の解法の定着と理解が浅い可能性が高い
【1】失点原因を克服する
❶ 曖昧な公式や定理が出された
失点の原因が公式・定理・定義の曖昧さにある場合は、該当単元の内容を見直し、対応する例題・類題を参考書で反復して知識として定着させましょう。
あわせて、網羅系の参考書学習の完成度が甘い傾向があるため、もう一度丁寧に復習してください。
❷ 問題の誘導に気づけなかった
解説を読むと解法は知っていたのに、誘導に気づけず解けなかったという場合は、演習量不足の可能性が高いです。
類題の演習を増やして、正攻法だけでなく別解にも取り組み、1問に対する解き方の手数を増やしましょう。
❸ 誘導での条件を使えなかった
誘導で与えられた条件をうまく活用できなかった場合、その単元の公式・定理・定義が持つ性質への理解が不十分な可能性があります。
参考書の単元冒頭にある公式・定理の導出方法や単元の定義を再確認し、原理から理解し直しましょう。
❹ 場合分け条件が不正確だった
問題の方針も解法の大筋も正しかったが、場合分けの条件設定を誤って失点したなら、到達度は高いものの詰めが甘い段階です。
なぜその場合分けになるのか、理由を自分の言葉で説明できるまで原理に立ち返って考えるようにしましょう。
【2】実戦と復習を重ねる
【1】で1回分の失点原因の分析と復習が終わったら、次は苦手克服ノートを作成しましょう。
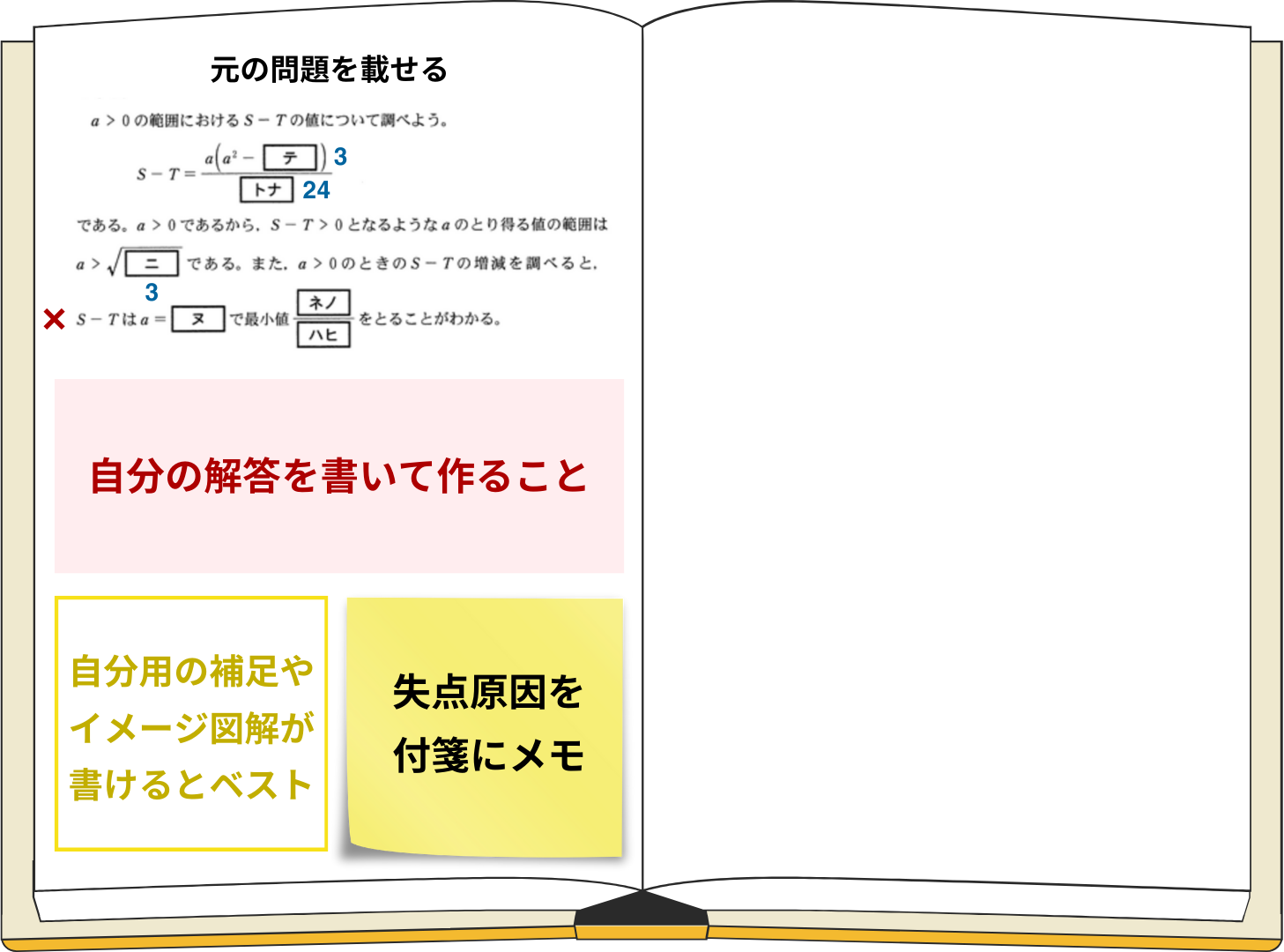
問題文や誘導過程を切り取って苦手ノートに貼りましょう。その際、誤答に至るまでの小問を正解していた場合は、その部分の解答は埋めたまま貼って構いません。
さらに、必ず自分で解答を書き込みましょう。解き直して解けるようになった後であれば、自分用のわかりやすい解答と図解なども追記できるはずです。
また、なぜ失点したのか、できなかった原因を付箋などに書いて解答の横に貼っておくと、自分の苦手要因を記録できるのでおすすめです。
定期的に苦手ノートを復習し、掲載されている問題に⚪︎が2つ付くまで繰り返しましょう。3日後、7日後、14日後、1ヶ月後という間隔での復習がおすすめです。
② 時間制限ありで8割を目指す
前述の【1】【2】を繰り返すと、時間無制限で8割を超えられる段階に至ります。次はいよいよ時間制限下(マーク時間を引いて55分で受ける)で8割を目指しましょう。
✔︎ 計算スピードを上げる
✔︎ ケアレスミスを減らす
計算スピードを上げるためには
・計算スピード自体を上げる
・計算過程の省略方法を知る
受験数学の計算スピードは、「計算そのものが速い」「計算過程の省略が上手い」の2要素から成ります。
前者は計算ドリル等の反復で鍛えられますが、後者の「上手な省略」は知識と経験によるもので、単なる計算練習だけでは身につきません。
たとえば
確率の余事象による解き方や、積分の1/6の公式などが計算過程の省略に該当する
この「計算過程の上手な省略」を体系的に学べる参考書が以下です。解くのが速く正確な数学の強者ほど、手を抜くべき所の見極めが巧みなのです。
ケアレスミスを減らすためには
ケアレスミスには人それぞれの傾向があります。自分がどのようなミスで失点しやすいかを把握しておけば、ピンポイントの対策が可能です。
読み取りミス型
✔︎ 誘導の文章や条件の見落とし
✔︎ 誘導の文章や条件の読み違え
対策方法
まずは問題文や誘導を流し読みし、数値や条件などの重要キーワードに線や丸で印をつけて強調し、いつも以上に注意深く目に入るよう工夫する
字を見間違え型
✔︎ 自分の書いた字を見間違える
✔︎ あちこちに書いて不明になる
対策方法
字の乱れで見間違える人は、普段から丁寧に書く意識を持ち、あちこちに書いて混乱する人は、暗算を取り入れて筆記量を減らす意識が大切
途中書き違え型
✔︎ なぜか次の式から値が変わる
✔︎ 合っているのに書き違える
対策方法
方針も計算も合っているのに、次の式で数値や符号、不等号の向きを書き違える人は、次の行を書いた直後に一行前の式を軽く目視する癖をつける
純粋計算ミス型
✔︎ 単純に計算ミスをしてしまう
対策方法
単純な計算ミスが多い場合は、暗算の精度がまだ低い可能性があるため、普段の数学演習で、簡単な計算から徐々に暗算の比率を増やして鍛える
ミスの原因を特定したら、ミスが減るまで対策を繰り返しましょう。どの型の対策でも、はじめは時間がかかっても丁寧に行い、徐々にスピードを上げる意識が大切です。
① ケアレスミスの傾向を分析する
② 該当型の対策を集中的に行う
③ 該当のミスが減るまで対策反復
Step3 共通テスト模擬で実戦
ここまでの流れで純粋な数学力は十分に身についています。次はいよいよ共通テスト形式ですが、センター試験との違いは、日常文から必要な条件を自力で抽出する点です。
手順1:時間制限なしで8割を目指す
手順2:時間制限ありで8割を目指す
マーク時間を引いた65分で実施
時間制限下で8割に届かない主な原因は、試験中に手が止まる時間が生じているためです。実戦時には、次の勉強法を取り入れてみてください。
手順1
時間制限ありの場合、試験中に手が止まって長く考え込んでしまった問題に印をつけておく
手順2
解答を確認する際に、印をつけた問題の”どの過程”に時間を費やしてしまったかを特定する
手順3
時間を失った原因となる弱点を集中的に対策し、次回以降は時間をとられないよう心がける
Step4 共通テスト過去問で配分
Step3まで達すれば、共通テスト形式で8割をとれることも出てくるでしょう。最後に、本番でも安定して8割を目指せるよう、自分ルールを定めておきましょう。
自分ルールとは
解く順番や時間配分、大問途中で行き詰まった際の対応など、想定外に備えて事前に自分なりのルールを決めておく
ルール① 共通テスト数学の時間配分
数学IAの場合
| 大問 | 配点 | 時間配分 |
|---|---|---|
| 第1問 | 30点 | 18分 |
| 第2問 | 30点 | 18分 |
| 第3問 | 20点 | 12分 |
| 第4問 | 20点 | 12分 |
| マーク・見直し | 10分 |
数学IIBCの場合
| 大問 | 配点 | 時間配分 |
|---|---|---|
| 第1問 | 15点 | 9分 |
| 第2問 | 15点 | 9分 |
| 第3問 | 22点 | 15分 |
| 選択1 | 16点 | 10分 |
| 選択2 | 16点 | 10分 |
| 選択3 | 16点 | 10分 |
| マーク・見直し | 7分 |
上の表はあくまで目安で、得意・不得意によって所要時間は多少前後します。自分なりに「この大問は⚪︎分まで」「この大問には最大⚪︎分かけてよい」といった絶対ルールを事前に決めておきましょう。
解けないとむしゃくしゃしますが、時間配分のルールを決めたらそのルールに従って解くことが、結局のところ総得点の安定につながります
ルール② 共通テスト数学の解く順番
開始直後に問題を見て、いきなり行き詰まることもあるでしょう。そこで焦って頭が真っ白になると、本来とれるはずの得点を落としかねません。
そうならないよう、その事態に直面したときの対処法をあらかじめ決めておきましょう。
単元別の得意不得意が激しい
単元ごとの得意不得意の差が激しいなら、得意な単元の大問から順に解くとよい
単元別の得意不得意に大差ない
単元ごとの得意不得意に大きな差がなければ、前から順に大問を解くのがおすすめ
今の合格可能性を診断
「今の勉強量のままで、第一志望に受かるのかな」など、今のパフォーマンスに不安を抱えていませんか?
ざっくりでも現在の合格可能性を知ることができたら…
現状がわからない中で勉強するのは、大きな不安とストレスを伴うものです。
そんな日々を奮闘する受験生向けに、1分で診断ができる「合格可能性診断」「合格に必要な勉強時間診断」をご用意しました。
今の自分と志望大学はどの程度かけ離れているのか、どれくらい勉強しなければならないのか。
目安を知りたい方は、以下のボタンタップからお手軽に診断してみてください。
今回の内容が参考になったという方は、下記の公式LINE登録から受験特典を受けとって、さらなる学習の向上に活かしてください。
基礎の徹底が超重要!
「自分のペースで勉強を進めているけれど、今のままでは受かる気がしない…」というお悩みを抱えていませんか?
同級生は成績も上がってきているのに…
このような不安に駆られ、”勉強に集中ができなくなった、勉強習慣が崩れた”という人をたくさん見てきました。そんなお悩みを解消するために、大学受験を乗り越えるための7つの無料特典をご用意しました。
5年以上にもわたり1000人以上の受験生の悩みと向き合ってきた経験、さらには筆者自身の受験経験をもとにした、公式LINE限定の7大特典です。
気になる方は、以下から特典内容を確認のうえ、公式LINEをご登録ください。



